Il metro di Sèvres, il meridiano terrestre e un lampo

 Il metro di Sèvres, il meridiano terrestre e un lampo
di Pasquale Falco

Achille, simbolo di rapidità, deve raggiungere la tartaruga,
simbolo di lentezza. Achille corre dieci volte più svelto della tartaruga
e le concede dieci metri di vantaggio. Achille corre quei dieci metri
e la tartaruga percorre un metro; Achille percorre quel metro,
la tartaruga percorre un decimetro; Achille percorre quel decimetro,
la tartaruga percorre un centimetro; Achille percorre quel centimetro,
la tartaruga percorre un millimetro; Achille percorre quel millimetro,
la tartaruga percorre un decimo di millimetro,e così via all’infinito;
di modo che Achille può correre per sempre senza raggiungerla.
Jorge Louis Borges

 Superate le difficoltà astronomiche grazie anche all’esperienza di Eratostene, gli uniformatori rivoluzionari affrontarono la problematica della misura della distanza tra due luoghi posti sulla superficie terrestre lungo lo stesso meridiano.

Giandomenico Cassini

Anche per questa difficoltà, sfruttarono esperienze e studi di cartografia e topografia, sviluppati in precedenza da altri scienziati.

Alla corte di Francia, ancora prima della rivoluzione, era stato dato ampio impulso per motivi militari alle scienze cartografiche giungendo a una prima, vera cartografia realizzata da uno Stato.

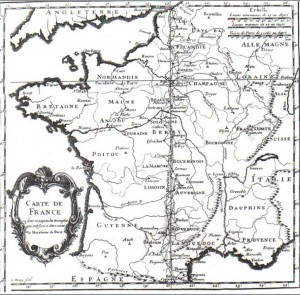
Furono i cartografi ed astronomi reali, Picard e Cassini (quest’ultimo, studioso bolognese trasferitosi alla corte francese e capostipite di quattro generazioni di valenti scienziati), che contribuirono alle prime affidabili rappresentazioni cartografiche della Francia. (FIGURA 1)
Fondamentale fu il tracciamento di una linea meridiana che attraversava tutta la Francia, da Dunkerque ai Pirenei, passata alla storia come meridiano di Parigi, rappresentato di seguito in una raffigurazione dell’epoca.

Incredibile a dirsi, tutto questo fu possibile sfruttando una semplice figura geometrica, il triangolo e il metodo cartografico che ne derivava, la triangolazione.

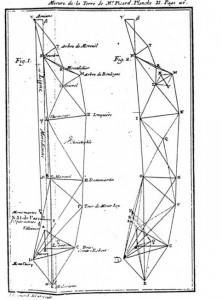
Questo metodo, introdotto qualche secolo prima dall’olandese Snellius, consente di misurare con precisione le distanze tra due luoghi molto lontani tra loro, collegandoli con degli ulteriori punti scelti sul terreno, fino a formare vere e proprie catene di triangoli aventi a due a due un lato in comune. ( FIGURA 2 )

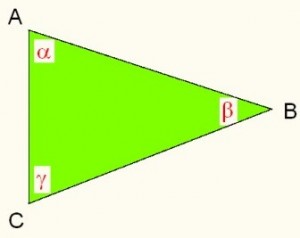
In pratica, volendo misurare la distanza tra due punti molto lontani tra loro, è possibile farlo, innanzitutto considerando un triangolo e ipotizzando che due suoi due vertici, A e B, coincidano con i due punti, e che il terzo vertice del triangolo, C, coincida con un terzo punto vicino ad A e facilmente raggiungibile.

FIGURA 1

Inizialmente si misura la distanza tra A e C, poi, posizionandosi in A, si calcola l’angolo α compreso tra B e C, e infine, posizionandosi in C, si misura l’angolo γ tra A e B: a questo punto si è in possesso di tutti i dati che consentono di calcolare i lati del triangolo e quindi anche la distanza tra A e B. ( FIGURA 3 )
Ebbene gli scienziati incaricati di portare a termine l’uniformazione del metro, Jean-Baptiste Delambre e Pierre Mèchain, scelsero come arco di meridiano terrestre quello tra Dunkerque, sul canale della Manica, e Barcellona, in Spagna; al termine di lunghe e faticose operazioni di campo condotte dal 1792 al 1799, con una catena di 90 triangoli ottennero la distanza tra i paralleli di delle due città.
Questa misura, unitamente ai calcoli astronomici, consentì di ottenere la misura prima dell’arco di meridiano e poi dell’intero meridiano; sulla base di tale ultima lunghezza fu realizzata la famosa barra di metallo, il campione dell’unità di misura della lunghezza, a cui fu dato il nome di metro (dal greco mètron, che vuol dire misura) e che venne conservata nell’Ufficio internazionale di Pesi e Misure a Sevrès, presso Parigi.

Storia finita direbbe qualcuno; anzi penserebbe che da quel momento in poi il metro, inteso come quarantamilionesima parte del meridiano terrestre, venisse introdotto grazie ai francesi in tutto i territori del vecchio continente. La risposta, invece, non è affermativa, o, meglio, lo è solo in parte, e tutto perchè nel frattempo era nata una ulteriore disputa astronomica.

In quell’epoca, infatti, si cominciò a dibattere anche sulla vera forma del nostro pianeta e si faceva strada l’idea che, anziché una sfera, la terra fosse

FIGURA 2

un ellissoide di rotazione regolare; oggi sappiamo che la terra ha una forma che per semplicità può essere riferita ad una tale figura geometrica, ma essa ha una forma molto più irregolare, con protuberanze e avvallamenti rispetto all’ellissoide di rotazione, definita geoide di rotazione.

Ebbene, i nostri rivoluzionari, per la sempre più convincente ipotesi che la terra fosse un ellissoide di rotazione con una sua eccentricità, e per il fatto che qualcuno già iniziasse a fornire misure di tale eccentricità determinando il valore dello schiacciamento ai poli, arrivarono alla deludente conclusione che i calcoli da loro effettuati fossero errati, perchè basati sull’errata ipotesi di un meridiano perfettamente circolare e su una terra perfettamente sferica. L’ulteriore amara conclusione cui si giunse fu che il metro di Sevrès non avesse quella tanto auspicata relazione con le dimensioni della terra e che era stato fallito il simbolico obiettivo di un metro campione pari effettivamente alla quarantamilionesima parte del meridiano terrestre.

A nulla valsero anche i vani tentativi di verifica dei calcoli e delle attività effettuate in campo.

Oggi gli studiosi grazie alla “teoria degli errori”, elaborata nel diciannovesimo secolo anche per gli stimoli ricevuti dalla grande impresa di misurazione del meridiano, sanno che in un qualsiasi processo di misura l’errore è una componente ineluttabile e che, anzi, un’attenta valutazione dell’errore può avvicinare al valore reale della misura; sulla base degli assunti della teoria degli errori, gli studiosi considerano le incongruenze delle misure di Delambre e Méchain non eccessivamente sostanziali, quantunque presenti.

FIGURA 3

All’epoca comunque, per non vanificare tutti gli sforzi fatti e rinunciare all’obiettivo che ci si era preposto, cioè quello di uniformare le misure attraverso una unità metrica unica, si arrivò alla pratica soluzione di battezzare il metro non più come la quarantamilionesima parte del meridiano terrestre, ma come una lunghezza esattamente pari a quella del metro campione conservato a Sevrès. A partire dal quel momento tutti i metri, in giro per il mondo, furono costruiti partendo dal quel metro campione di Sevrès.

In conclusione di questa narrazione, occorre aggiungere che nel ventesimo secolo è stata avvertita sempre più la necessità di riprodurre l’unità campione senza dover per forza di cose rapportarsi alla barra campione di Sevrès.

Così nel 1983, grazie alle sofisticate strumentazioni di laboratorio di cui si dispone, si decise di ridefinire il metro sulla base della velocità della luce nel vuoto, definendolo come la distanza percorsa dalla luce nel vuoto in 1/299.792.458 di secondo.

Verrebbe proprio voglia di affermare che un metro, in definitiva, corrisponde ad un lampo!

Napoli, 21 dicembre 2021